前言:
這部分要來講的是高中很常出現的符號,如果你是要找如何算出項,或是求,可能就要請你去看上集,我會把連結放在文章下方,到時候再請你連過去囉。
=====如果公式沒有跑出來的話麻煩稍微等一下喔~=====
這個符號讀作Sigma,中文唸作西格瑪
定義:
三大性質:
性質1:
推導:
性質2:
推導:
左式=,
因為乘法分配律,所以可以把提出來,
變成,
性質3:
推導:
左式=,
因為加法有交換率,所以可以先把先分別加起來,再做加(減),
變成,
然後再把他們換成Sigma
考試愛考的三大公式 :
1.
2.
3.
公式3可以利用公式1來幫助記憶,但把公式2做平方不會得到4次方的公式呦
3.
公式3可以利用公式1來幫助記憶,但把公式2做平方不會得到4次方的公式呦

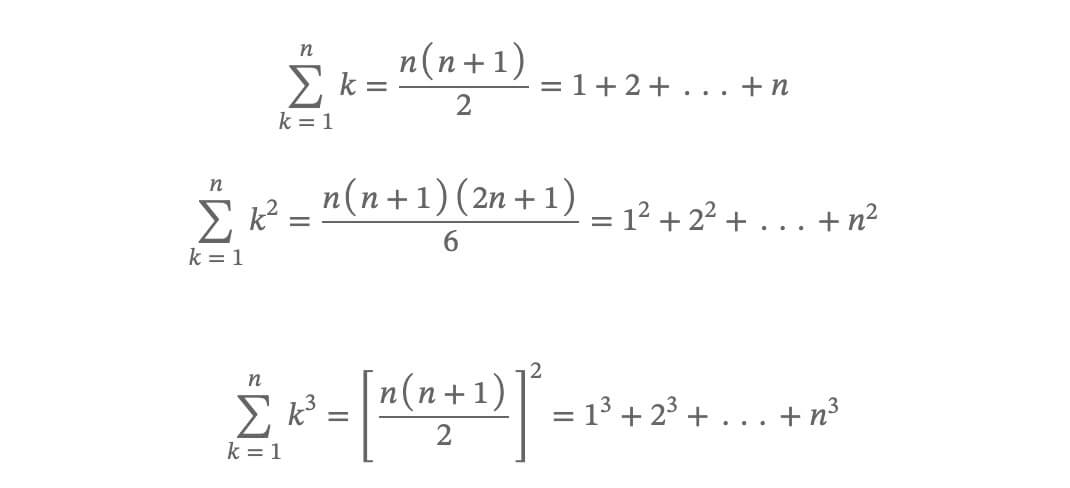







0 留言